Re: 1
Posted: Thu Jan 19, 2012 11:42 am
Grizzly 1023
The focal point for Texas firearms information and discussions
https://mail.texaschlforum.com/
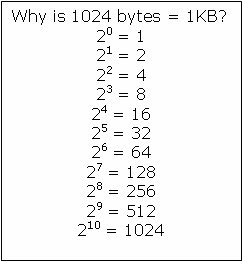


It is also a duplicate of the post immediately before yours.MoJo wrote:1024 is the natural number following 1023 and preceding 1025.
1024 is a power of two: 210 (2 to the 10th power).[1] It is the lowest power of two requiring four decimal digits, and the lowest power of two containing the digit 0 in its decimal representation (excluding any leading zeroes).
It is also the square of 32: 322.
1024 is the smallest number with exactly 11 divisors (but note that there are smaller numbers with more than 11 divisors; e.g., 60 has 12 divisors (sequence A005179 in OEIS).

Great minds run in the same channels!The Annoyed Man wrote:It is also a duplicate of the post immediately before yours.MoJo wrote:1024 is the natural number following 1023 and preceding 1025.
1024 is a power of two: 210 (2 to the 10th power).[1] It is the lowest power of two requiring four decimal digits, and the lowest power of two containing the digit 0 in its decimal representation (excluding any leading zeroes).
It is also the square of 32: 322.
1024 is the smallest number with exactly 11 divisors (but note that there are smaller numbers with more than 11 divisors; e.g., 60 has 12 divisors (sequence A005179 in OEIS).

And there are 10 kinds of people in the world, those who understand binary, and those who don't.MoJo wrote:Great minds run in the same channels!The Annoyed Man wrote:It is also a duplicate of the post immediately before yours.MoJo wrote:1024 is the natural number following 1023 and preceding 1025.
1024 is a power of two: 210 (2 to the 10th power).[1] It is the lowest power of two requiring four decimal digits, and the lowest power of two containing the digit 0 in its decimal representation (excluding any leading zeroes).
It is also the square of 32: 322.
1024 is the smallest number with exactly 11 divisors (but note that there are smaller numbers with more than 11 divisors; e.g., 60 has 12 divisors (sequence A005179 in OEIS).